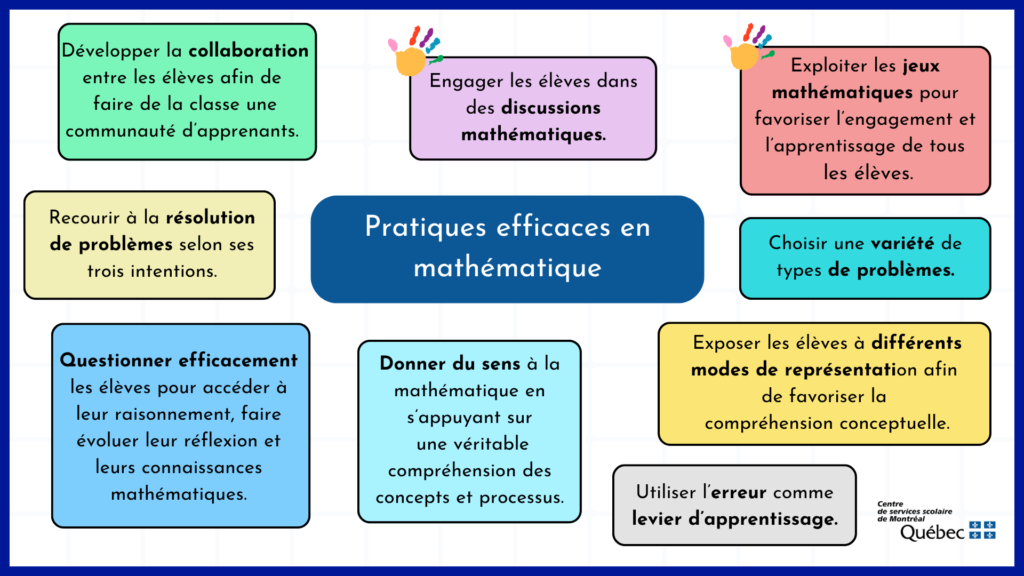
Voici 9 pratiques efficaces en mathématique qui sont les plus susceptibles d’avoir un impact sur la réussite de chacun de vos élèves. Chaque pratique est issue de recherches probantes, a été testée dans des contextes éducatifs et a démontré des effets positifs en termes d’amélioration de la réussite des élèves.

Autoformation du CSSDN qui explique ce qu’est une causerie et ce qui ne l’est pas (lien à venir)

capsule d’autoformation portant sur la variété de type de problèmes et le jugement professionnel

Autoformation sur les trois intentions de la résolution de problèmes

L’importance de la compréhension conceptuelle dans l’acquisition des faits numériques

Les bienfaits d’établir des relations positive en classe
Nombreuses ressources concernant la collaboration

Pratiquer les maths comme les mathématiciens

Relier les savoirs d’aujourd’hui à l’apprentissage de demain
L’art de questionner de façon efficace

Document produit par l’équipe des programmes d’études de mathématique
Apprendre et évaluer autrement/Questions à se poser

Balado Les éclaireurs– Radio-Canada, Louise Poirier
